A.
Teorema
Sisa
1)
F(x) =
(x – b)· H(x) + S,
maka S = F(b)
2)
F(x) =
(ax – b)· H(x) + S,
maka S = F(b/a)
3)
F(x) : [(x – a)(x – b)],
maka S(x)
= (x – a)S2 + S1, dengan S2 adalah sisa
pembagian pada tahap ke–2
Dengan H(x): Hasil pembagian
dan S: sisa pembagian
B.
Teorema
Faktor
(x – b) adalah
faktor dari f(x) bila S = f(b) = 0
C.
Akar
Rasional Persamaan Suku Banyak
Bentuk umum : axn
+ bxn –1 + cxn –2 + … + d = 0. Akar–akarnya adalah x1,
x2, …, xn.
1)
x1
+ x2 + …+ xn = -b/a
2)
x1
· x2 · …· xn = d/a(bila berderajat genap)
3)
x1
· x2 · …· xn = -d/a(bila berderajat ganjil)
4)
x1
· x2 + x1 · x3 + x2 · x3 + … = c/a
D. Cara Horner/bangun/skema/sintetik
Misalkan suku banyak f(x) = ax3 + bx2 + cx + d. Jika akan ditentukan nilai suku banyak x = k, maka:f(x) = ax3 + bx2 + cx + df(x) = (ax2 + bx + c)x + df(x) = ((ax + b)x + c)x + dSehingga f(k) = ((ak + b)k + c)k + d.Bentuk tersebut dapat disajikan dalam bentuk skema berikut ini.
Agar lebih memahami tentang cara Horner, pelajarilah contoh soal berikut.
Contoh soal
Hitunglah nilai suku banyak untuk nilai x yang diberikan berikut ini.
1. f(x) = x3 + 2×2 + 3x – 4 untuk x = 5
2. f(x) = 2×3 – 3×2 + 9x + 12 untuk x = ½
Contoh soal
Hitunglah nilai suku banyak untuk nilai x yang diberikan berikut ini.
1. f(x) = x3 + 2×2 + 3x – 4 untuk x = 5
2. f(x) = 2×3 – 3×2 + 9x + 12 untuk x = ½
Penyelesaian :
Jadi nilai suku banyak f(x) untuk x = 5 adalah 186.
Jadi, nilai suku banyak f(x) untuk x = ½ adalah 16.
INGAT !!!
• Masing-masing koefisien x disusun dari pangkat terbesar sampai terkecil
(perpangkatan x yang tidak ada, ditulis 0).
• Tanda panah pada skema berarti mengalikan dengan k, kemudian dijumlahkan dengan koefisien yang berada di atasnya.
• Masing-masing koefisien x disusun dari pangkat terbesar sampai terkecil
(perpangkatan x yang tidak ada, ditulis 0).
• Tanda panah pada skema berarti mengalikan dengan k, kemudian dijumlahkan dengan koefisien yang berada di atasnya.
Contoh Soal :
Soal No. 1
Diberikan suku banyak
F(x) = 3x3 + 2x − 10.
Dengan cara substitusi, tentukan nilai dari F(2)
Soal No. 1
Diberikan suku banyak
F(x) = 3x3 + 2x − 10.
Dengan cara substitusi, tentukan nilai dari F(2)
Pembahasan
Masukkan nilai x = 2 untuk F(x).
F(x) = 3x3 + 2x − 10
F(2) = 3(2)3 + 2(2) − 10
F(2) = 24 + 4 − 10 = 18
Soal No. 2
Diberikan suku banyak
F(x) = 3x3 + 2x − 10.
Dengan cara Horner, tentukan nilai dari F(2), cocokkan dengan jawaban nomor soal nomor 1 di atas!
Pembahasan
Cara Horner:
Setelah 3 turun ke bawah, kemudian di kali 2, hasilnya 6. Jumlahkan dengan angka di atasnya, hasilnya kemudian kalikan 2 lagi dst. Hasil akhirnya F(2) = 18, cocok dengan jawaban hasil nomor 1.
Soal No. 3
Diketahui bahwa (x − 1) adalah faktor dari persamaan x3 − 2x2 − 5x + 6 = 0.
Tentukan faktor-faktor yang lain!
Pembahasan
x − 1 merupakan faktor dari x3 − 2x2 − 5x + 6 = 0, sehingga x = 1 adalah akar dari persamaan tersebut.
Pembahasan
x − 1 merupakan faktor dari x3 − 2x2 − 5x + 6 = 0, sehingga x = 1 adalah akar dari persamaan tersebut.
Untuk mencari faktor lain gunakan horner seperti berikut:
Pemfaktoran dengan horner untuk nilai x = 1
Diperoleh bahwa
koefisien x2 adalah 1
koefisien x adalah −1
dan 6
Sehingga faktor yang didapat adalah
1x2 − 1x − 6 = 0
x2 − x − 6 = 0
Faktorkan lagi, lebih mudah karena x dalam pangkat dua, diperoleh
x2 − x − 6 = 0
(x + 2)(x − 3) = 0
Jadi selain (x − 1) , faktor-faktor dari x3 − 2x2 − 5x + 6 = 0 adalah (x + 2) dan (x − 3)
Soal No. 4
Diketahui x = 1 adalah akar dari persamaan suku banyak 2x3 − 9x2 + 13x − 6 = 0. Tentukan akar-akar yang lain dari persamaan di atas!
Pembahasan
2x3 − 9x2 + 13x − 6 = 0
2x2 − 7x + 6 = (2x − 3)(x − 2)
2x − 3 = 0
x = 3/2
x − 2 = 0
x = 2
Jadi akar-akar yang lain adalah 3/2 dan 2
Soal No. 5
Diketahui;
2x3 − 9x2 + 13x − 6 = 0
Jika x1, x2 dan x3 adalah akar-akar dari persamaan di atas, tentukan:
a) hasil kali akar-akar
b) jumlah akar-akar
Pembahasan
Ax3 + Bx2 + Cx + D = 0
Jika x1, x2 dan x3 adalah akar-akar dari persamaan di atas, tentukan:
a) hasil kali akar-akar
b) jumlah akar-akar
Pembahasan
Ax3 + Bx2 + Cx + D = 0
maka berlaku
a) x1 ⋅x2 ⋅ x3 = − D/A = − (−6)/2 = 6/2 = 3
b) x1 + x2 + x3 = − B/A
= − (−9)/2 = 9/2
Soal No. 6
Diketahui;
b) x1 + x2 + x3 = − B/A
= − (−9)/2 = 9/2
Soal No. 6
Diketahui;
2x4 + 5x3 − 11x2 − 20x + 12 = 0
Jika x1, x2 , x3 dan x4 adalahakar-akar dari persamaan di atas, tentukan:
a) hasil kali akar-akar
b) jumlah akar-akar
Pembahasan
Ax4 + Bx3 + Cx2 + Dx + E = 0
Jika x1, x2 , x3 dan x4 adalahakar-akar dari persamaan di atas, tentukan:
a) hasil kali akar-akar
b) jumlah akar-akar
Pembahasan
Ax4 + Bx3 + Cx2 + Dx + E = 0
maka berlaku
a) x1 ⋅x2 ⋅ x3 ⋅ x4 = E/A = (12)/2 = 6
b) x1 + x2 + x3 + x4 = − B/A
= −(5)/2 =− 5/2
Soal No. 7
Salah satu faktor suku banyak P(x) = x4 −15x2 −10x + n adalah (x + 2) . Faktor lainnya adalah...
A. x − 4
B. x + 4
C. x + 6
D. x − 6
E. x − 8
(UN 2008)
Pembahasan
Tentukan lebih dulu nilai n dari suku banyak di soal. Jika x + 2 adalah faktor, maka x = − 2 jika dimasukkan persamaan di atas akan menghasilkan P(x) = 0.
P(x) = x4 −15x2 −10x + n
b) x1 + x2 + x3 + x4 = − B/A
= −(5)/2 =− 5/2
Soal No. 7
Salah satu faktor suku banyak P(x) = x4 −15x2 −10x + n adalah (x + 2) . Faktor lainnya adalah...
A. x − 4
B. x + 4
C. x + 6
D. x − 6
E. x − 8
(UN 2008)
Pembahasan
Tentukan lebih dulu nilai n dari suku banyak di soal. Jika x + 2 adalah faktor, maka x = − 2 jika dimasukkan persamaan di atas akan menghasilkan P(x) = 0.
P(x) = x4 −15x2 −10x + n
0 = (−2)4 −15(−2)2 −10(−2) + n
n = 24
Sehingga P(x) secara lengkap adalah
Sehingga P(x) secara lengkap adalah
P(x) = x4 −15x2 −10x + 24
Uji pilihan hingga mendapatkan nilai P(x) sama dengan nol seperti ini
A. x − 4 → x = 4 → P(x) = (4)4 −15(4)2 −10(4) + 24 = 0
B. x + 4 → x = − 4 → P(x) = (−4)4 −15(−4)2 −10(−4) + 24 = 80
C. x + 6 → x = − 6 → P(x) = (−6)4 −15(−6)2 −10(−6) + 24 = 840
dan seterusnya
Terlihat yang menghasilkan P(x) = 0 adalah untuk x = 4, sehingga faktor lainnya adalah (x − 4).
Uji pilihan hingga mendapatkan nilai P(x) sama dengan nol seperti ini
A. x − 4 → x = 4 → P(x) = (4)4 −15(4)2 −10(4) + 24 = 0
B. x + 4 → x = − 4 → P(x) = (−4)4 −15(−4)2 −10(−4) + 24 = 80
C. x + 6 → x = − 6 → P(x) = (−6)4 −15(−6)2 −10(−6) + 24 = 840
dan seterusnya
Terlihat yang menghasilkan P(x) = 0 adalah untuk x = 4, sehingga faktor lainnya adalah (x − 4).
Dicoba:
Soal No. 8
Suku banyak P(x) = x3 + ax2 - 13x + 10 mempunyai faktor linear (x - 2). Faktor linear yang lain adalah…
A. (x - 5)
B. (x + 1)
C. (x + 2)
D. (x - 1)
E. (x - 4)
Soal No. 8
Suku banyak P(x) = x3 + ax2 - 13x + 10 mempunyai faktor linear (x - 2). Faktor linear yang lain adalah…
A. (x - 5)
B. (x + 1)
C. (x + 2)
D. (x - 1)
E. (x - 4)
Soal No. 9
Jika f(x) dibagi dengan (x – 2) sisanya 24, sedangkan jika f(x) dibagi dengan (2x – 3) sisanya 20. Jika f(x) dibagi dengan (x – 2) (2x – 3), sisanya adalah....
A. 8x + 8
B. 8x − 8
C. −8x + 8
D. −8x − 8
E. −8x + 6
(UN 2007)
Pembahasan
Misal sisa pembagian dari f(x) dirumuskan S(x) = ax + b
Dibagi dengan (x – 2) sisanya 24 artinya:
x – 2 = 0
x = 2
S(x) = ax + b
24 = 2a + b ..........(Persamaan 1)
Dibagi dengan (2x – 3) sisanya 20 artinya:
2x – 3 = 0
x = 3/2
S(x) = ax + b
20 = 3/2 a + b ..........(Persamaan 2)
Gabungkan persamaan 1 dan 2
24 = 2a + b
20 = 3/2 a + b
______________ −
4 = 1/2 a
a = 8
24 = 2a + b
24 = 2(8) + b
24 = 16 + b
b = 8
S(x) = 8x + 8
Soal No. 10
Diketahui suku banyak P(x) = 2x4 + ax3 − 3x2 + 5x + b. . Jika P(x) dibagi (x − 1) sisa 11, dibagi (x + 1) sisa -1, maka nilai (2a+ b) =...
A. 13
B. 10
C. 8
D. 7
E. 6
(UN 2011)
Pembahasan
Untuk (x − 1)
x = 1 → P(x) = 11
2(1)4 + a(1)3 − 3(1)2 + 5(1) + b = 11
2 + a − 3 + 5 + b = 11
a + b = 7 .............(Persamaan 1)
Untuk (x + 1)
x = − 1 → P(x) = − 1
2(−1)4 + a(−1)3 − 3(−1)2 + 5(1) + b = −1
2 − a − 3 − 5 + b = − 1
− a + b = 5 ..........(Persamaan 2)
Dari Persamaan 1 dan 2
a + b = 7
− a + b= 5
__________ +
2b = 12
b = 12/2 = 6
a + b = 7
a + 6 = 7
a = 1
Sehingga
2a + b = 2(1) + 6 = 8
Read more: http://matematikastudycenter.com/kelas-11-sma/98-suku-banyak-dan-teorema-sisa#ixzz4FWm7Lbi8
Jika f(x) dibagi dengan (x – 2) sisanya 24, sedangkan jika f(x) dibagi dengan (2x – 3) sisanya 20. Jika f(x) dibagi dengan (x – 2) (2x – 3), sisanya adalah....
A. 8x + 8
B. 8x − 8
C. −8x + 8
D. −8x − 8
E. −8x + 6
(UN 2007)
Pembahasan
Misal sisa pembagian dari f(x) dirumuskan S(x) = ax + b
Dibagi dengan (x – 2) sisanya 24 artinya:
x – 2 = 0
x = 2
S(x) = ax + b
24 = 2a + b ..........(Persamaan 1)
Dibagi dengan (2x – 3) sisanya 20 artinya:
2x – 3 = 0
x = 3/2
S(x) = ax + b
20 = 3/2 a + b ..........(Persamaan 2)
Gabungkan persamaan 1 dan 2
24 = 2a + b
20 = 3/2 a + b
______________ −
4 = 1/2 a
a = 8
24 = 2a + b
24 = 2(8) + b
24 = 16 + b
b = 8
S(x) = 8x + 8
Soal No. 10
Diketahui suku banyak P(x) = 2x4 + ax3 − 3x2 + 5x + b. . Jika P(x) dibagi (x − 1) sisa 11, dibagi (x + 1) sisa -1, maka nilai (2a+ b) =...
A. 13
B. 10
C. 8
D. 7
E. 6
(UN 2011)
Pembahasan
Untuk (x − 1)
x = 1 → P(x) = 11
2(1)4 + a(1)3 − 3(1)2 + 5(1) + b = 11
2 + a − 3 + 5 + b = 11
a + b = 7 .............(Persamaan 1)
Untuk (x + 1)
x = − 1 → P(x) = − 1
2(−1)4 + a(−1)3 − 3(−1)2 + 5(1) + b = −1
2 − a − 3 − 5 + b = − 1
− a + b = 5 ..........(Persamaan 2)
Dari Persamaan 1 dan 2
a + b = 7
− a + b= 5
__________ +
2b = 12
b = 12/2 = 6
a + b = 7
a + 6 = 7
a = 1
Sehingga
2a + b = 2(1) + 6 = 8
Read more: http://matematikastudycenter.com/kelas-11-sma/98-suku-banyak-dan-teorema-sisa#ixzz4FWm7Lbi8
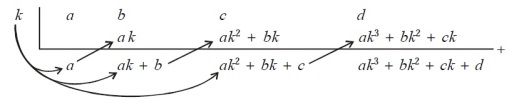
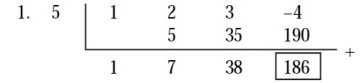
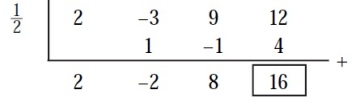




Komentar ini telah dihapus oleh pengarang.
BalasHapusPlay Online Casino Games for Free With $5000 Bonus
BalasHapusPlay Online Casino Games for Free With 1xbet korean $5000 Bonus at Shootercasino. casino games you can play 10bet for free with no registration or 카지노 registration required!
PRAGMATIC CASINO - Casinos, Gaming & Promos | Mapyro
BalasHapusFind your way around the casino and find out 속초 출장안마 where everything is located. 태백 출장샵 There 정읍 출장마사지 are a few casino 충청북도 출장마사지 and dining 부천 출장안마 options you may find at the